Efficiency comparison of horizontal axis wind turbines and bladeless turbines
Antranig Bardakjian 1*, Paul Mandadakis2 and Amy Tingle3
University of Technology Sydney, P.O Box 123, MaPS, Broadway NSW 2007.
1 E-Mail: antranig.t.bardakjian@student.uts.edu.au
2 E-Mail: paul.mandadakis@student.uts.edu.au
3 E-Mail: amy.tingle@student.uts.edu.au
* Author to whom correspondence should be addressed; E-Mail: antranig.t.bardakjian@student.uts.edu.au
DOI: http://dx.doi.org/10.5130/pamr.v4i0.1461
Abstract: The purpose of this meta study is to determine whether bladeless wind turbines are more efficient than horizontal axis wind turbines. Using resources such as research papers, online articles and academic papers from different academic databases provided by UTS library, a comparison between these wind turbines was constructed. Using Weibull’s equation, it was found that horizontal axis wind turbines are still more efficient. Although bladeless are more cost efficient, offshore horizontal axis wind turbines produce more energy at lower wind speeds, due to the ratio between power usage to power output of approximately 80% for bladed turbines and approximately 70% for bladeless turbines. More research needs to be done on how to increase the efficiency of these wind turbines.
Keywords: horizontal axis wind turbines; bladeless turbines; efficiency

Copyright 2017 by the authors. This is an Open Access article distributed under the terms of the Creative Commons Attribution 4.0 Unported (CC BY 4.0) License (https://creativecommons.org/licenses/by/4.0/), allowing third parties to copy and redistribute the material in any medium or format and to remix, transform, and build upon the material for any purpose, even commercially, provided the original work is properly cited and states its license.
1. Introduction
As non-renewable sources decline, the need for renewable sources increases. Efficient renewable sources of energy are important as non-renewable sources, such as fossil fuels. With these resources declining, alternative methods of generating electrical energy are becoming more sought after. One current technology already providing an alternative method are wind turbines. Current wind turbines take advantage of a naturally occurring, renewable system to generate electricity. There are many different types of wind turbines currently in use, but this paper will focus on the more commonly produced horizontal axis wind turbine (HAWT) (fig 1) and comparing them to the recently developed bladeless turbines.
1.1 HAWT
Figure 1. General outline of HAWT [1]
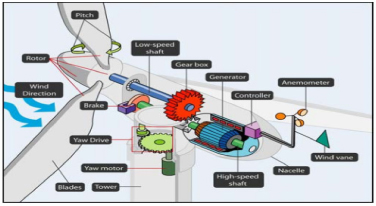
Figure 2. Components of HAWT[3][4]
HAWT are the most commonly produced wind turbines [1] and are currently very efficient at converting the kinetic energy of wind into electrical energy. Wind passing over the turbine blades causes them to spin due to the wind’s force and magnitude. This effect is explained by Bernoulli’s theorem, which relates to fluid dynamics. This focuses on the relationship between velocity, pressure, viscosity, density and elevation. In the case of a HAWT the flow of air is horizontal and therefore elevation becomes irrelevant. The difference in height between the top and bottom of the blade is also insignificant, leaving pressure and velocity as the only significant parameters. Per Bernoulli’s theorem[2], when there is no change in the gravitational potential energy of a fluid, a decrease in pressure is associated with an increase in velocity.
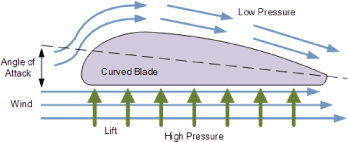
Figure 3. As the wind moves over the blade, it creates a difference in pressures and that is what causes the motion of the blade [6]
The blade of a turbine has a cambered design meaning that the top and bottom of the blade are asymmetrical and curved. Due to this shape, the velocity of the air on either side of the blade will be different. The air passing below the blade slows down, whilst the air passing over the top will speed up [6] [7]. Going back to Bernoulli’s theorem [2], at a point of low velocity, in this case the bottom of the wing, there will be an area of high pressure. At the top of the wing, the air is moving faster, creating an area of low pressure. When this happens, lift is generated and will cause the turbine to spin. The faster the wind flows, the lower the pressure on the top of the blade will be. This means the blade will rotate faster as there is less pressure on the top of the blade to inhibit the motion caused by the high pressure area. As recent as early 2017, the blades rotate at approximately 18 rpm [8]. At this speed, not enough useful energy is generated, so a series of gears are used to increase the speed by a factor of a hundred [5] [8], allowing useful energy to be generated as well as counteracting the effects of the high entropy system. These turbines are currently highly effective, converting 80% [1] [4] of the wind energy into electrical energy.
The main problem with the HAWT is that there are many moving components (fig 2) which need replacing multiple times throughout its lifespan. For instance, the gearbox needs replacing every 1.5 years [4]. With HAWT’s life span between 20-25 years [4], it will require between 13-17 gearboxes which continually adds onto the maintenance of the HAWT.
The entropy of a system depends on the size density and predictability of a system [11]. Small, dense systems such as nuclear reactors have a rather predictable energy flow and are said to have a low entropy. Wind however, is a large, unpredictable and inconsistent system. Wind speed and direction are factors that are constantly changing from one moment to another due to factors like the seasons and the associated tidal pull and coastal winds. Relating this back to Bernoulli’s theorem [2], the change in certain wind factors will affect the speed at which the turbine moves and therefore the output energy. HAWT’s design helps counteract the high entropy of the wind due to its ability to adjust the speed of the rotor and thus producing a consistent output of electrical energy.
1.2 Bladeless Turbines

Figure 4. Prototype of Bladeless wind turbines, Spain [9] [12]
Bladeless turbines are a relatively new concept, roughly 5 years, which takes advantage of an aerodynamic effect called vorticity. This effect is one engineers always design to avoid as it causes structures to oscillate and eventually collapse. Bladeless turbines however take advantage of this effect.
When wind breaks against the turbine the wind flows down the side of the turbine in a circular motion called a vortex. This creates areas of high and low pressures surrounding the turbine which cause it to oscillate. When wind is slow and steady, it breaks against the turbine. Making the vortices uniform and the oscillations caused by them therefore will also be uniform. However, as the wind speed increases, the vortices that are created become erratic and irregular. This means that the frequency at which the turbine is oscillating is in a state of flux. Wind tunnel studies on the turbines have shown that when they are placed close together they can feed off each other (fig 5). The vortices given off by the first turbine interact with the next turbine which helps create oscillations [25].
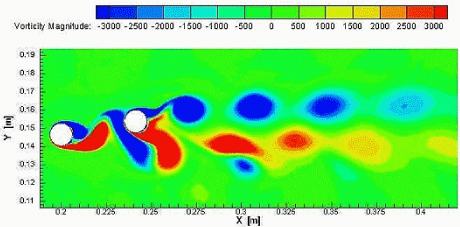
Figure 5. Beneficial vorticity effect on two cylinders [13]
The size of the turbine also affects the uniformity of the vortices created. Wind speed, and hence pressure, varies with altitude. If a large turbine is made, wind of varying velocities would be acting on it. This will give rise to oscillations in the turbine of various frequencies. Given that wind is a high entropy system [11], and that this turbine’s efficiency is dependent on the regularity and consistency of the parameters of the system, this will greatly affect its efficiency.
The kinetic energy associated with these oscillations is then converted to electrical energy. There are less components to this design, which lower the maintenance levels of the turbine. Compared to the HAWT, bladeless turbines have a have a lower efficiency rate, around 70% [10]
1.3 Efficiency of onshore horizontal axis wind turbines
The papers researched were analysis of countries such as Nigeria [14] [15], China [16] and India [17] have been undertaken to determine the efficiency of different onshore locations to place HAWTs. The papers use a combined method of mathematically computing the Weibull parameters, detailed in 3.1.1, taking field data of the wind speeds over a period and borrowing information from certain agency such as the Nigerian Meteorological Agency (NIMET) [15]. As well as measuring, which heights are effective at producing more power, the papers also use various types of wind turbines not limiting themselves to one model.
1.4 Efficiency of offshore horizontal axis wind turbines
Further research was undertaken of HAWT analysis has been undertaken to determine whether there is promise in offshore locations in Malaysia[18] and India [19] [20]. The papers once again use a method gathering field data, by satellite and by sensors, and by calculations from the Weibull function. With the turbines being out on the coast the altitude is considered the hub height of the turbine as the sea level height is negligible.
1.5 Efficiency of bladeless turbines
Being a relatively new area of exploration there is a smaller range of papers related to efficiency of bladeless turbines. However, the papers used for this meta study use a standard method of gathering field data all year long in the Netherlands [21]. Using quantitative formulations, the shaking force can be directly correlated to the power the bladeless turbines output as seen in 3.2.1
Figure 6. Geographic representation of papers researched
2. Methods
This meta-study was performed using different academic databases, journals and website articles. The research and data used came from these different mediums like databases such as Academic Search Complete, Science Direct, SCOPUS, and other sources such as Google Scholar. To narrow the results, some search terms included “vorticity”, “wind turbines”, “bladeless wind turbines”, “wind power assessment”, “wind turbine location”. Journals found were mostly restricted to the past 10 years as this is a relatively new development in renewable energy.
The research was conducted in two portions, focusing on HAWTs and their performance in different situations and the efficiency of bladeless turbines. Papers that had some relevance but not directly to the subject matter at hand were filtered out or were kept as reference material listed in the appendices.
3. Results and Discussion
3.1. Efficiency of horizontal axis wind turbines
3.1.1 Mathematical Analysis
Two different variables are to be calculated to determine the wind efficiency; wind speed and power.
Wind speed
The Weibull function is a way of calculating wind speed and is expressed in Equation 1:
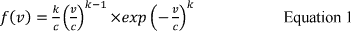 [15]
[15]
Where k and c are parameters from Equation 1, the dimensionless parameter and the speed parameter (m/s) respectively. Vm is the wind speed (m/s). Each of these variables need to be calculated separately as seen below.
 [15]
[15]
Vm is the wind speed on average (m/s) seen in Equation 3 and σ is the standard deviation from the average speed (m/s) seen in Equation 4. Calculating k gives an idea of close to peak the wind speed is.
 [15]
[15]
 [15]
[15]
Vm and σ are calculated with the basic mean and standard deviation formulas shown in Equation 3 and 4 respectively with n showing the amount of measurements taken and vi being the value of the individual wind speed measured (m/s).
 [15]
[15]
Using values calculated before c can be derived with vm which is the mean of the wind speed (m/s) and k which is the dimensionless parameter.
Wind Power
The wind speed is reliant on one of the variables mentioned above, wind speed and also the area that the blades themselves occupy as shown in Equation 6:
 [16]
[16]
ρ is the air density at the wind turbine (kg/m3), A is the area of the blades (m3) and v3 is the wind speed cubed (m3/s3).
The wind power density can be derived with the values from Equation 6.
 [16]
[16]
P(v) is the wind power calculated from before as well A equating to the area of the blades. f(v)dv is the Weibull function and these values are integrated from zero to infinity.
3.1.2 Results for Onshore Turbines
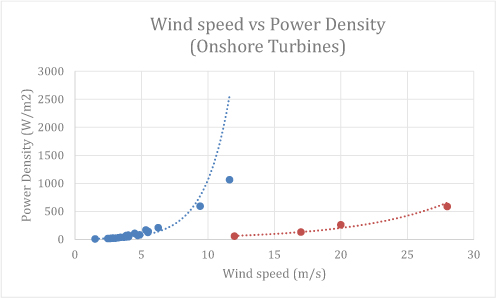
Figure 7. Relationship between wind speed and power density of onshore turbines, showing a double exponent.
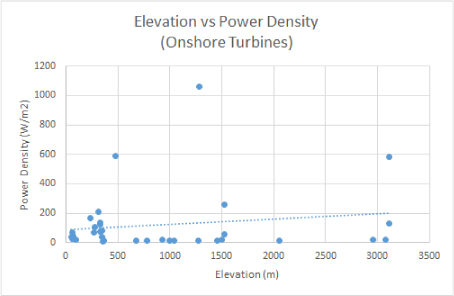
Figure 8. Relationship between elevation and power density of onshore turbines.
As can be seen from the results there is a greater impact from the onshore wind speed on the power density than there is from the onshore elevation of the turbine.
The onshore wind speed graph has an increasing exponential effect ranging from 200 - 1800 W/m2 which is split into two curves indicating the different rates of the different locations but both have a general exponential shape.
The onshore elevation graph however, has a shallow linear shape with a few outlier above it indicating a smaller range of influence when compared to the onshore wind speed graph of only 0 - 400 W/m2.
3.1.3 Results for Offshore Turbines
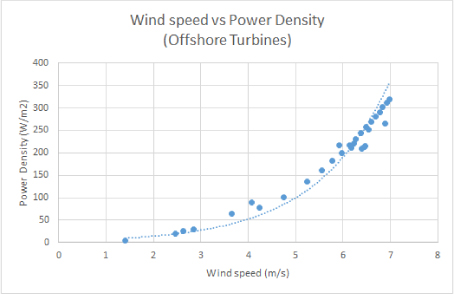
Figure 9. Relationship between wind speed and power density of offshore turbines.
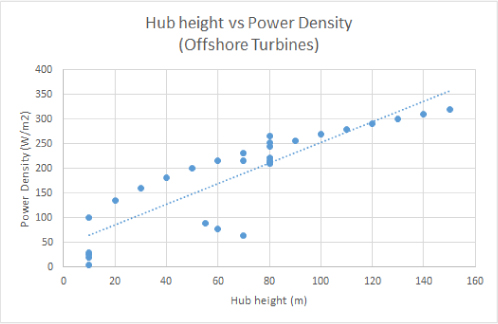
Figure 10. Relationship between hub height and power density of offshore turbines.(what outliers are)
From these results a similar result can be seen such that once again the offshore wind speed has more of an impact to power density, relative to the previous onshore graphs, then there is from the offshore elevation of the turbine.
The offshore wind speed graph has a smaller range than previous, only 0 - 400 W/m2, having greater amount of influence than the offshore elevation graph due to its exponential shape. The offshore elevation graph uses a different measure of height as all the turbines are at the shore line the hub of the turbine is considered instead. The range corresponds to 0 - 400 W/m2 but the growth is linear having less of an effect than the offshore wind speed.
Comparing the two wind speed graphs and taking similar points, such as onshore having 20m/s produce 400 W/m2 and offshore having 7m/s produce the same amount (400 W/m2) the offshore turbines are more efficient when it comes to wind speed.
With both elevation graphs they have a similar range of 0 - 400 W/m2 however the offshore turbines require less elevation to achieve the same power density making it more efficient.
Overall the offshore turbines show promise in their ability to produce power with slower winds and lower altitudes.
3.2 Efficiency of bladeless turbines
3.2.1 Mathematical analysis
The shaking motion of a bladeless turbine can be directly related to simple harmonics as seen in Equation 8:
 [22]
[22]
F is the force of the harmonic motion (N), k is the spring constant (N/m) and x the displacement distance (m).
Differentiated Equation 8 gives:
 [22]
[22]
m is the inertial mass (kg) of the oscillating body and t is time (second)
Solving the differential equation above leads to Equation 10:
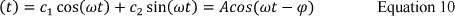 [22]
[22]
c1 and c2 are constants, A is the amplitude from the equilibrium position (m), ω = 2πυ is the angular frequency, and φ is the phase.
The kinetic energy of the bladeless turbines equates to Equation 11:
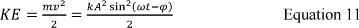 [22]
[22]
and the potential energy equates to Equation 12:
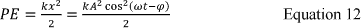 [22]
[22]
Combining the two equations for mechanical energy we get:
 [22]
[22]
Which divided by time gives power (W)
 [22]
[22]
3.2.2 Results for Bladeless Turbines
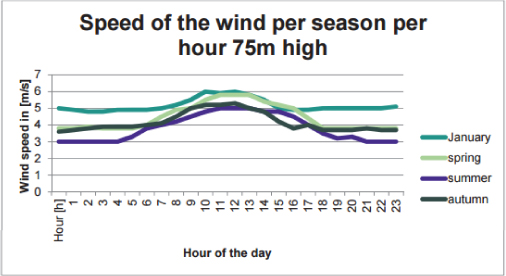
Figure 12. Wind speed analysis over seasonal days (24)
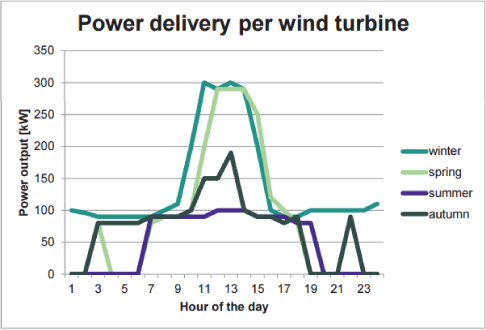
Figure 13. Power output over seasonal days (24)
Looking at Figures 13 and 14 it can be said that the bladeless turbines are less efficient than the bladed turbines as they require greater power to run, in the megawatts range (24). While they behave like HAWTs and perform more efficiently when they are stronger winds in the end the HAWTs can deliver more for less power.
Looking at all the factors the most effective turbines are the ones bladed offshore that as they require slower winds to deliver power and they do not need high elevation to get results. This can eliminate construction difficulties as they are very few suitable areas on Earth where high elevated are suitable. Instead choosing to build these turbines near coast near countries such as India or Malaysia closer to the high winds these turbines need to perform is a more effective strategy. Whilst there are some downsides such as spatial limitations that the HAWTs take up due to their structure, until the bladeless turbine catch up in their efficiency this is not a viable option to yield maximum results.
4. Conclusions
After conducting research, the results concluded that a single bladeless turbine is 30% less efficient than a HAWT. This is due to the physical system design as well as its lack of ability to counter the high entropy of wind. Due to their small size, they make better use of the area they occupy as more can be placed in the same area as HAWTs. This aspect bridges the gap between the two turbines and make up for their lack of efficiency. Although HAWTs are more efficient they require more maintenance due to the increased number of components and moving parts. This includes gears and braking systems. Bladeless turbines have no moving parts or connections which greatly minimizes maintenance. From the gathered data, the greater the velocity of the wind acting on the HAWT the greater the output that is given. The bladeless turbines however work best when wind velocity is lower as this will result in uniform vortices. In the end the offshore HAWTs prove to be the most efficient in power output due to their need for slower winds and lower elevation to yield results.
Acknowledgments
We would like to acknowledge Jurgen Schulte for teaching us the material needed. Blake Regan and Liam Martin for helping with the formatting and writing the paper. The UTS library staff with sourcing and proper referencing of the papers and journals used. UTSEpress for printing and publishing our paper and our Energy Science and Technology students for their support and encouragement throughout this process.
References and Notes
1. Manwell JF, McGowan JG, Rogers AL. Introduction: Modern Wind Energy and its Origins. Wind Energy Explained: John Wiley & Sons, Ltd; 2009. p. 1-22. doi: https://doi.org/10.1002/9781119994367
2. Encyclopædia B. Bernoulli’s theorem. Available at: https://www-britannica-com.ezproxy.lib.uts.edu.au/science/Bernoullis-theorem. Accessed April, 20, 2017.
3. A tutorial on the dynamics and control of wind turbines and wind farms. Proceedings of the American Control Conference; 2009.
4. Turbines Info. Horizontal Axis Wind Turbine - HAWT. 2011; Available at: http://www.turbinesinfo.com/horizontal-axis-wind-turbines-hawt/. Accessed 04/24, 2017.
5. Desjardins J. Animation: How Wind Turbines Work. Available at: http://www.visualcapitalist.com/animation-how-wind-turbines-work/. Accessed April, 31, 2017.
6. Renewable-teachers b. Science of Wind Generation. Available at: https://renewableteacher.wordpress.com/the-science-behind-wind-generation/. Accessed April, 20, 2017.
7. University oC. how things really work. Available at: https://phys.org/news/2012-01-wings.html. Accessed April, 21, 2017.
8. U.S Department of Energy. Energy 101: Wind Turbines - 2014 Update. 2014; Available at: https://youtu.be/EYYHfMCw-FI. Accessed 04/28, 2017
9. McKenna P. Bladeless Wind Turbines May Offer More Form Than Function. 2015; Available at: https://www.technologyreview.com/s/537721/bladeless-wind-turbines-may-offer-more-form-than-function/. Accessed April, 30, 2017.
10. Luciano M. Bladeless Turbines: The Future Of Wind Energy Harvesting? 2017; Available at: http://search.proquest.com.ezproxy.lib.uts.edu.au/science/docview/1875962473/2D30BECD61954365PQ/3?accountid=17095#. Accessed 04/28, 2017.
11. Leavitt R. entropy-the key to stability. Available at: http://positiveenergy.blogspot.com.au/2009/03/entropy-key-to-stability.html. Accessed April, 21, 2017.
12. Markham D. This giant straw is actually a vertical bladeless wind turbine. 2015; Available at: https://www.treehugger.com/wind-technology/vortex-vertical-bladeless-wind-turbine.html. Accessed 04/28, 2017.
13. Noger, C. Aeroacoustic and Aerodynamic Researches, Available at: http://c.noger.free.fr/Anglais/cyl_aero_acou_en.php, Accessed 05/03, 2017
14. Adaramola MS, Oyewola OM. Evaluating the performance of wind turbines in selected locations in Oyo state, Nigeria. Renewable Energy 2011 12;36(12):3297-3304.
15. Ayodele TR, Ogunjuyigbe ASO, Amusan TO. Wind power utilization assessment and economic analysis of wind turbines across fifteen locations in the six geographical zones of Nigeria. J Clean Prod 2016 8/15;129:341-349. doi: https://doi.org/10.1016/j.jclepro.2016.04.060
16. Li C, Liu Y, Li G, Li J, Zhu D, Jia W, et al. Evaluation of wind energy resource and wind turbine characteristics at two locations in China. Technology in Society 2016 11;47:121-128. doi: https://doi.org/10.1016/j.techsoc.2016.09.003
17. Chandel SS, Ramasamy P, Murthy KSR. Wind power potential assessment of 12 locations in western Himalayan region of India. Renewable and Sustainable Energy Reviews 2014 11;39:530-545. doi: https://doi.org/10.1016/j.rser.2014.07.050
18. Albani A, Ibrahim MZ. Wind Energy Potential and Power Law Indexes Assessment for Selected Near-Coastal Sites in Malaysia. Energies (19961073) 2017 03;10(3):1-21.
19. Murthy KSR, Rahi OP. Preliminary assessment of wind power potential over the coastal region of Bheemunipatnam in northern Andhra Pradesh, India. Renewable Energy 2016 12;99:1137-1145. doi: https://doi.org/10.1016/j.renene.2016.08.017
20. Nagababu G, Kachhwaha SS, Savsani V, Banerjee R. Evaluation of offshore wind power potential in the western coast of India: a preliminary study. Current Science (00113891) 2017 01/10;112(1):62-67.
21. Green energy based inductive Self-Healing highways of the future. 2016 IEEE Transportation Electrification Conference and Expo (ITEC); 2016.
22. Patel S. New Approach Powers Bladeless Wind Turbine. Power 2015 07;159(7):14-16.
Appendices